Stopped Clock Paradox; Relativity Down for the Count

[Carleas]

@James S Saint

Why would the station see something different than what is there

It doesn’t, it just sees it at a different time. Light carrying the information from the face of the clock not only arrives at the observer on the train at a different time than it arrives at the station observer, it leaves the face of the clock at different times for each observer. This isn’t an artifact of light taking time to travel; the moment in which the light leaves the face of the clock is different in the two frames, so even though they see the same image conveyed by that light, the observers “see” it as having occurred at a different time.

Again, you’ve picked an unlikely situation and are balking at the counter-intuition of it. The observer who throws the clock on the train would need to see the clocks accelerated from 0 to .5c over the course of a minuscule fraction of a second to ‘see’ the change in time on the clocks. And even then, the change is not very large. It should be counter-intuitive to witnesses something that out of the ordinary.

[James_S_Saint]

@Carleas

@James S Saint

Why would the station see something different than what is there

It doesn’t, it just sees it at a different time. Light carrying the information from the face of the clock not only arrives at the observer on the train at a different time than it arrives at the station observer, it leaves the face of the clock at different times for each observer. This isn’t an artifact of light taking time to travel; the moment in which the light leaves the face of the clock is different in the two frames, so even though they see the same image conveyed by that light, the observers “see” it as having occurred at a different time.

So you are saying that light shining from far above, an instantaneous flash from the Sun, would reflect off of two identical reading clocks on a train, but when that image got to an observer an equal distance away from each clock, those images would somehow have changed into different images?

The flash from the Sun will get to each clock at a particular time reading and thus capture an image as it reflects away. No matter where the observer is standing, how would the light know how to change that image from a reading of “3:00” to “4:00”, especially if it has to change that image differently depending on where the observer happens to be standing?

If we think in terms of 2 photo flashers at the station that are equal distance from the 2 clocks on the train and flash at t = tF rather than the Sun, the light traveling from each will reach the train’s clocks in the same amount of time. They each capture an instantaneous image of the clocks then reflect light in all directions. Obviously all observers around the station, regardless of their position, will see the same 2 images.

Anticipating your repeated phrase, “the train will not see the flashes as being synchronous”, let me point out that we are not talking about what the front clock sees from the back flasher. Each clock has its own flasher that is equally distant. So this isn’t an issue of how far apart the clocks are or how synchronized the flasher would appear to be by the train. The light reaches each clock from the same distance, nearly zero. Thus the image captured is an independent issue for each clock. The clocks and images don’t care about synchronization of other flashers or clocks.

Also each flasher is only concerned with its own associated clock. Each flasher sees its clock travel 110 meters from a different origin, thus calculate the same t’ from the same t,x and the time dilation issue will be the same for each flasher and clock. If one flasher sees that its clock is 10 seconds behind, the other flasher will have to see that its clock is also 10 seconds behind.

The train sees its clocks always reading identically. If the light from each flasher gets to each clock in the same amount of time from the flashers (being equally far from each clock), how could the train see the 2 flashes come to the clocks at different times? The x value for the photo flashers to the train would be identical for each clock. The ∆x between the clocks along the track is irrelevant because there is no motion in the direction from the photo flashers to the clocks. So what would be the equation for that?

If the train doesn’t see time dilation concerning the flashers, then the image captured would have to be the same and be seen as the same by all station observers.

[James_S_Saint]

And then reversing the direction of the flash should not affect any timing concern, thus;

[Carleas]

Why are you using ∆x and ∆t in your diagram? ∆x and ∆t aren’t relevant to demonstrating relativity of simultaneity, you introduced them to try and show that the Lorentz transformation only applied at the origin (which we’ve shown not to be the case).

How does adding more flashers to the station elucidate anything? To show relativity of simultaneity, we only need three clocks: station, train A, and train B. Why multiply elements? (That’s not rhetorical. As far as I can tell, they complicate the question without providing useful information; what useful information do you see them providing in the example?)

From your diagrams, it seems that you reject the idea of “lines of simultaneity”, but they follow directly from the Lorentz transformation equations. Have we given up on those equations?

In your most recent example, in which frame are you setting the clocks to be equal? You seem to be alternately stipulating that they are equal in either frame, but you can’t stipulate both within the same example. To decrease ambiguity, I’d ask that you clearly state which clocks you’re stipulating to be synchronized, because otherwise when I say “[some observer] will not see the flashes as being synchronous,” you’re liable to say “no, because we stipulated that [some observer]'s clocks were synchonized.”

The flash from the sun is a somewhat different case, because for that it’s reasonable to say that the clocks accelerated from rest during the time it took the light to travel from the sun to the earth. We’ve been dealing with a situation when the flash occurs when the train is already at speed.

[James_S_Saint]

@Carleas

Why are you using ∆x and ∆t in your diagram?

To demonstrate that there is no simultaneity issue.

@Carleas

∆x and ∆t aren’t relevant to demonstrating relativity of simultaneity, you introduced them to try and show that the Lorentz transformation only applied at the origin (which we’ve shown not to be the case).

Of course they aren’t “relevant to demonstrating relativity of simultaneity”, because we have no relativity of simultaneity to demonstrate. YOU introduced them to stay away from simultaneity on the same train as I said that you would have to do, yet still claimed that you never do that.

So I take it that we are back to political debating where honesty is not required?

@Carleas

From your diagrams, it seems that you reject the idea of “lines of simultaneity”, but they follow directly from the Lorentz transformation equations. Have we given up on those equations?

We do not need those equations at all as I said from the beginning. Since it is clear to me that you insist on misusing them so as to create a simultaneity issue, I merely provided an example where they are not needed at all.

I claimed that you were misusing Lorentz. I provided equation examples using it my way and your way demonstrating that the way you insisted on would provide incorrect results and we agreed those were incorrect results. Rather than point to anything that was wrong with anything I provided, you merely provided equations doing it the right way and then claimed that you are right. We argued for about 15 pages without you ever showing me one detail that was wrong with what I provided while I pointed to explicit detail of what you were doing incorrectly.

So I have shown you 2 pics that are extremely clear as to what is going on and they need no Lorentz at all. The first pictorial shows 3 scenarios that together form the whole picture of the station-train scenario of the OP except for the direction of the flashing. The second pictorial shows the reversed flashing that results in the exact scenario of the OP.

The first part shows a clock being tossed onto the train at the back of the railcar and that clock being photo flashed after it got to 4:00-t at ∆x, ∆t.

The second part shows a similar event on a different train. The clock is identical but it is thrown onto the front of the railcar and then travels the exact same ∆x, ∆t distance and also gets photo flashed. Because the figures are identical, we don’t care what their value is. We get the same results for any value of ∆x, ∆t.

The third part shows that we can merely do the same thing on one train and see both photo flashes seeing a time reading from the train of 4:00-t from both clocks.

Since both clocks travel the same amount ∆x, ∆t, they must have the same reading on the train when photo flashed.

Finally in the other pictorial, we merely reverse the flashing from toward the train, to from the train to demonstrate the original flashing issue of the OP.

The 2 pictorials very clearly display that anyone at the station in any position at all would see an image of 4:00-t from both clocks.

A) What do you see incorrect with the first third of the pictorial labeled, “Train Clock Synchronicity”?
B) What do you see incorrect with the second part of that pictorial?
C) What do you see incorrect with the third part of the pictorial?
D) What do you see incorrect with the pictorial labeled, “Flash Synchronicity”?

[Carleas]

A, B, C, and D) None of these diagrams shows more than one frame of reference.

[James_S_Saint]

@Carleas

A, B, C, and D) None of these diagrams shows more than one frame of reference.

None of them need to. Why do you want to complicate the obvious?

I didn’t tell you what the oil pressure in the engines was either.

In this example, the 2 flashers flash synchronously. There is only one image to be seen. If they show 4:00-t anywhere, they show 4:00-t everywhere, including on board the train.

And;

The question in the OP isn’t WHAT is seen.
The OP paradox is WHEN it is seen.

[Carleas]

@James S Saint

The question in the OP isn’t WHAT is seen.
The OP paradox is WHEN it is seen.

Exactly. So it doesn’t matter that “there is only one image to be seen,” it’s seen at different times for different frames of reference.

How would you solve for the time dilation without the Lorentz transformation?

[James_S_Saint]

@Carleas

@James S Saint

The question in the OP isn’t WHAT is seen.
The OP paradox is WHEN it is seen.

Exactly. So it doesn’t matter that “there is only one image to be seen,” it’s seen at different times for different frames of reference.

Note that in the OP, it is discussed that the light (image) must travel to both frames, yet one frame is moving (at least one), thus one will not see them simultaneously. The paradox is about which one will see them simultaneous and which will not. But all clocks read the same at that moment.

The photo images are from the train’s own clocks. The station’s clock at any other moment would read differently. It is only at that one moment that both the train’s and the station’s clocks read the same (which really isn’t a requirement for a paradox to occur). But the time for the image to get back to center for both train and station is the same.

@Carleas

How would you solve for the time dilation without the Lorentz transformation?

∆t’ is the difference in the train’s time between any 2 coordinates.
∆t is the difference in the station’s time between the same 2 coordinates.

td, time dilation, is ∆t’/∆t

You can’t tell what dt actually is because you are not given the velocity of the train, but then it doesn’t matter what it is. The paradox comes into play for any velocity.

[Carleas]

So solve it with the givens from the OP.

[James_S_Saint]

@Carleas

So solve it with the givens from the OP.

Why? It isn’t needed for anything. All you need to know is that the train is moving with respect to the station. Even if there were no time dilation, you would still have a paradox.

You can’t resolve the engine’s oil pressure either. It is equally as relevant.

[Carleas]

Can you please express the paradox mathematically? Show how any equations produce conflict results.

Also, I found some equations for constant acceleration, but they’re only for x=t=0. It says so, explicitly, in the article.

@"[url=http://en.wikipedia.org/wiki/Time_dilation#Time_dilation_at_constant_acceleration

Wiki[/url]"]Assuming the spaceship’s position at time t = 0 being x = 0…

[James_S_Saint]

@Carleas

Can you please express the paradox mathematically? Show how any equations produce conflict results.

Well, I showed them in “Answer 1”, but let’s see…

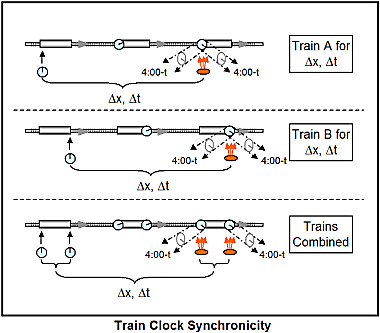
Timer F travels a distance of ∆x resulting in a ∆t at a position xF0+∆x.

Timer B starts behind timer F on the x-axis. Timer B travels at the same velocity, v, and an equal distance of ∆x resulting in an equal ∆t at a position xB0+∆x.

If both timers were set to be equal to T0 at xF0 and xB0, each timer will read T0+∆x, which we declare to be 4:00-t.

The train will see its timers reading 4:00-t when they flash or are flashed upon. The station will see that same image.

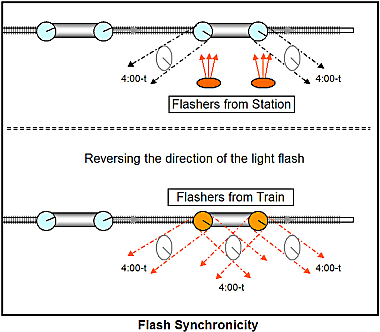
The question becomes, which, if either will see the flash from both timers reach it at the same moment if the observers are centered between the flashes at the moment of flashing.

The station observer must see both flashes at 4:00-t + tds, where “tds” is the time of travel for the photons to the station’s clock.

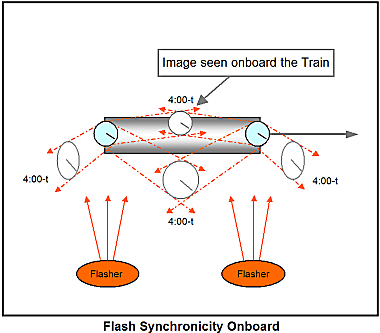
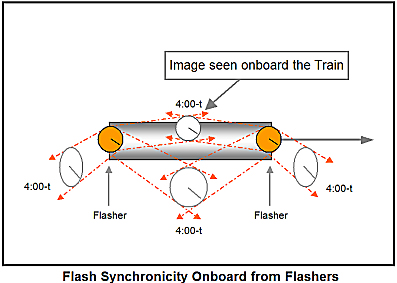
The train must see both flashes at 4:00-t + tdr, where “tdr” is the time of travel for the photons to the centered train clock.

The problem is that one, if not both, of the clocks are moving with respect to the flashed images (or photons in the OP).

So the time it takes for the timer B flash to get to the station clock is “tdsB” and reaches the station at 4:00-t+tdsB.

The time it takes for the timer F flash to get to the station clock is “tdsF” and reaches the station at 4:00-t+tdsF.

Since the station clock is centered at the time of flash;
tdsB = tdsF

Since the train clock is centered at the time of flash;
tdrB = tdrF

Since the clocks are centered, we can assign xdr to be the distance to the train clock from either flasher.

But from the station’s perspective, during the time dtr and dts, the train is moving, thus;
xdrB = dtr + vdtr, and
xdrF = dtr - vdtr

So from the station’s perspective;
tdrB = xdrB/v = (tdr + vtdr)/v = tdr/v + tdr = tdr + tdr/v, and
tdrF = xdrF/v = (tdr - vtdr)/v = tdr/v + tdr = tdr - tdr/v

Thus from the station’s perspective to see the train clock stop;
tdr/v + dtr = tdr/v - dtr

and that could only be true if the train wasn’t moving.

But from the station’s perspective, during the time dtr and dts, the train is moving, thus;
xdrB = dtr + vdtr, and
xdrF = dtr - vdtr

So from the train’s perspective;
tdsB = xdsB/v = (tds + vtds)/v = tds/v + tdr = tds + tds/v, and
tdsF = xdsF/v = (tds - vtds)/v = tds/v + tds = tds - tds/v

Thus from the station’s perspective to see the train clock stop;
tds/v + tds = tds/v - tds

and that could only be true if the station wasn’t moving.

There is your paradox in equation form.

As I said at the very beginning of the OP, that is all of the math required.

[Carleas]

@James S Saint

If both timers were set to be equal to T0 at xF0 and xB0, each timer will read T0+∆x, which we declare to be 4:00-t.

I assume you mean t0+∆t? You’re adding a distance to a time otherwise.

@James S Saint

The train will see its timers reading 4:00-t when they flash or are flashed upon. The station will see that same image.

Point of clarification: “see that same image” means that they perceive that the flash occurs when the timer reads 4:00-t. It does not mean they see the image at the same time as measured by their own clock. Otherwise, you are begging the question.

The stipulation, just to be explicit, is that the flashers are set to be synchronized in the train’s frame?

@James S Saint

The station observer must see both flashes at 4:00-t + dts, where “dts” is the time of travel for the photons to the station’s clock.

This is why it needs to be explicit. We have stipulated that they go off at t in the train’s frame, but that does not mean they go of at the same time

The information carried by the flashes says that they occur at 4:00-t in the train’s frame, but that occurs at time 4:00-t’. The light from the flashers reaches the station observer at 4:00-t’ + dt’ (where dt’=t1’-t0’, dt’ is the time it took the photon to travel in the station frame, which is the difference in time between where the flashers go off and where the light his the station observer.

I’ll pause here to make sure we’re still on the same page.

[James_S_Saint]

@Carleas

@James S Saint

If both timers were set to be equal to T0 at xF0 and xB0, each timer will read T0+∆x, which we declare to be 4:00-t.

I assume you mean t0+∆t? You’re adding a distance to a time otherwise.

Correct. i was getting my t’s and d’s and x’s all mixed up.

@Carleas

@James S Saint

The train will see its timers reading 4:00-t when they flash or are flashed upon. The station will see that same image.

Point of clarification: “see that same image” means that they perceive that the flash occurs when the timer reads 4:00-t.

They don’t “perceive” it until the light reaches them. But the light will be sent out at 4:00-t (station time).

@Carleas

The stipulation, just to be explicit, is that the flashers are set to be synchronized in the train’s frame?

I think the original stipulation was that the station is centered when they both flash. Considering this pictorial;

And this one;

Obviously they will both read identically from both perspectives.

@Carleas

The information carried by the flashes says that they occur at 4:00-t in the train’s frame, but that occurs at time 4:00-t’.

No. It is stipulated to be the station’s referenced time, but the clocks were set such that (4:00-t)’ would be the same as the station at that moment. So (4:00-t)’ = (4:00-t).

Summery of the Setup
To summarize the scenario setup, let me go through it again with less explanation.

A station clock is set so that at 4:00-t a railcar will be passing by. On that railcar, fore and aft, two flashers are set to go off exactly when the station clock will be reading 4:00-t and also when they are equal distance from the station clock with respect to the station clock’s reference frame. So by design, the station clock must see both flashers trigger at exactly 4:00-t.

Also aboard the train, a train clock is set to be exactly centered between the two flashers when the station clock reads 4:00-t by its own reference frame regardless of how the station reference frame might view it. The train clock is then adjusted so that it too will read exactly 4:00-t at that same moment.

Thus at 4:00-t as read by either clock, both flashers are designed to flash. Simultaneity of the flashing and centeredness of the clocks from their own reference frames are guaranteed by setup design.

@Carleas

The light from the flashers reaches the station observer at 4:00-t’ + dt’ (where dt’=t1’-t0’, dt’ is the time it took the photon to travel in the station frame, which is the difference in time between where the flashers go off and where the light his the station observer.

I noted it as “tds”.

dt’ doesn’t really mean much when referring to light travel. The light doesn’t care about anyone else’s reference frames nor do the reference frames when it comes to light travel.

[Carleas]

@James S Saint

(4:00-t)’ = (4:00-t).

OK, so the stipulation is that the station sees all the timers as going off at 4:00-t, and we are trying to solve for what time the train sees the flashers as going off? Because you set tB and tF in the train frame, but now you seem to be stipulating their time in the station’s frame.

[James_S_Saint]

@Carleas

@James S Saint

(4:00-t)’ = (4:00-t).

OK, so the stipulation is that the station sees all the timers as going off at 4:00-t, and we are trying to solve for what time the train sees the flashers as going off? Because you set tB and tF in the train frame, but now you seem to be stipulating their time in the station’s frame.

In that sentence, “station sees”, meant the station,s reference frame, not seeing from the light traveling to the station clock.

The time they are seen to go off is irrelevant. The question is which one will perceive both flashers as simultaneous, regardless of whatever time they might be reading. It is an issue of the time and distance of the light travel. I have shown them all reading 4:00-t just to show that they obviously all can read the same. It doesn’t matter in which frame I set them, as per;

[Carleas]

@James S Saint

I have shown them all reading 4:00-t just to show that they obviously all can read the same. It doesn’t matter in which frame I set them, as per;

As I’ve said for a long time, they all can read 4:00-t, but not in the same run for two observers in moving frames. It is possible to set the starting conditions so that either the train or the station read all clocks as at 4:00-t. It is not possible to do it at the same time (edit: that is, in the same run), and to do so is to beg the question of the paradox, i.e. it is to assume the paradox, not conclude it.

[James_S_Saint]

@Carleas

@James S Saint

I have shown them all reading 4:00-t just to show that they obviously all can read the same. It doesn’t matter in which frame I set them, as per;

As I’ve said for a long time, they all can read 4:00-t, but not in the same run for two observers in moving frames. It is possible to set the starting conditions so that either the train or the station read all clocks as at 4:00-t. It is not possible to do it at the same time, and to do so is to beg the question of the paradox, i.e. it is to assume the paradox, not conclude it.

So then tell me what is incorrect about that pictorial. Because according to that pictorial, they certainly CAN all read the same.

[Carleas]

It only shows one frame of reference.

Look at the diagram below. The blue coordinate frame is equivalent to the train’s frame, and the “rod (time, zero)” can be thought of as the front half of the train at t=t’=0. The white coordinate frame is equivalent to the station frame.

This diagram shows both frames, which yours does not.