Is a coin more likely to flip tails if it has already flipped heads a bunch?

[Flannel_Jesus]

Just a little bit of genuine interest would do. Interest in your own code.

[PZR]

One doesn’t dare sympathize, for it is clearly beyond one.

[PZR]

But it must be most terrible, most annoying, to have to deal with lowly misers.

I can only wish God’s vengeance upon them, for placing obstacles in the roads of true mastery and excellence.

[PZR]

We will go back to our own clearly inferior and inadequate musings on probability and statistics, surely sullying the very world a master may walk.

[PZR]

Which would basically put us here.

Obviously not addressed to the truly advanced and genius minds.

[PZR]

But to despicable rabble.

[Flannel_Jesus]

I learned something absolutely fascinating and tragic today: the gambler’s fallacy is on record as leading to some deaths in Italy.

No 53 puts Italy out of its lottery agony | World news | The Guardian.

@The Guardian

After not showing for almost two years, number 53 was pulled out of the basket in the Venice lottery on Wednesday night.

All over Italy people had placed increasingly huge bets on the elusive number in recent months, more and more convinced that it had to appear.

In a frenzy that even lottery-mad Italy has rarely seen, some 53 addicts ran up debts, went bankrupt, and lost their homes to the bailiffs.

Four died in 53-related incidents. A woman drowned herself in the sea off Tuscany leaving a note admitting that she had spent her family’s savings on the number. A man from Signa near Florence shot his wife and son before killing himself. A man was arrested in Sicily this week for beating his wife out of frustration at debts incurred by his 53 habit.

In all, more than €3.5bn (£2.4bn) was spent on 53, an average of €227 for each family. In January alone, €671.9m was spent.

Although 53 had come up in other regional lotteries, it had not appeared in Venice since May 2003, and Wednesday was the 153th draw. The government will pay out around €600m in winnings to an unspecified number of winners.

[MagsJ (Surya Loka)]

.

Mad!

[Carleas]

@PZR

If each flip was 50 50, you would expect at least 50% of instances of 10 mill flips where the state just stays heavy forever.

This doesn’t follow. If each flip was 50-50, some would stay tails-heavy forever, some would stay heads-heavy forever, and some would go back.

@PZR

Each individual flip cannot be 50 50 and at the same time overall flip composition be 50 50. If a break from overall 50 50 happens, and individual flips remain 50 50, there is no reason it would trend back to balance. In f act, it might be likelier to just stay on the twisted path it entered. Of course, even this wouldn’t hold, what would hold is a kind of unpredictable perfect variance with no possible predictable overall composition.

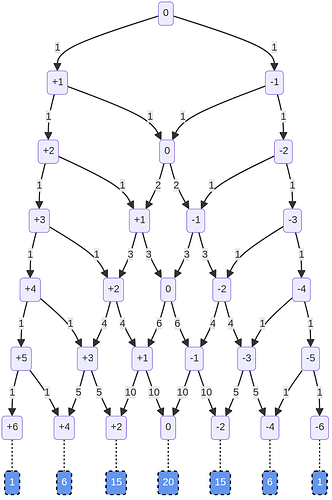
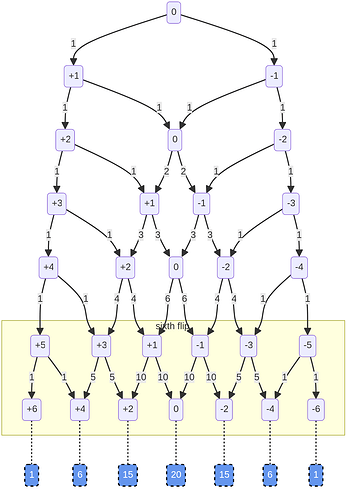
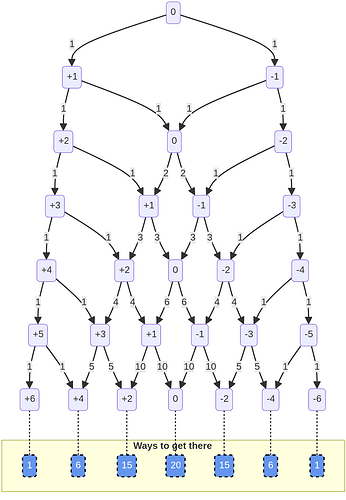
You’re going to hate this, but I made another chart:

This should help explain why the overall composition is predictable even though the flips are random.

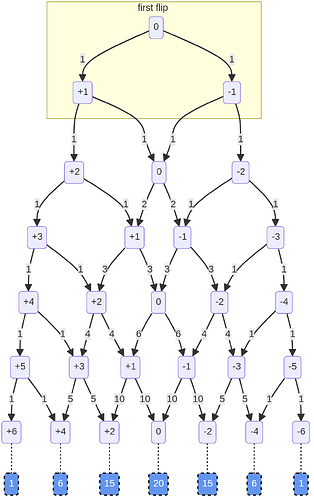
The numbers in the boxes are ‘heaviness’, where heaviness = heads-tails. So we start at 0, and the first flip leaves at +1 (heads) or -1 (tails):

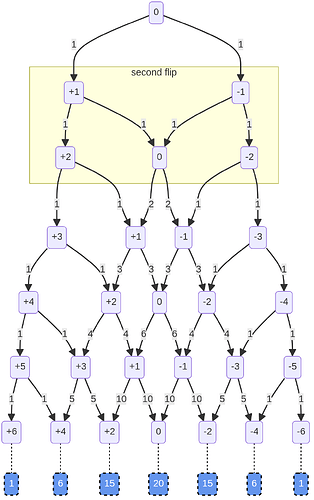
The numbers along the arrows count the number of ways to get to that arrow: on the first flip, there’s two paths, and one way to get to each: one heads or one tails. Same on the second flip: because none of the paths has crossed yet, there’s only one way to get to each path:

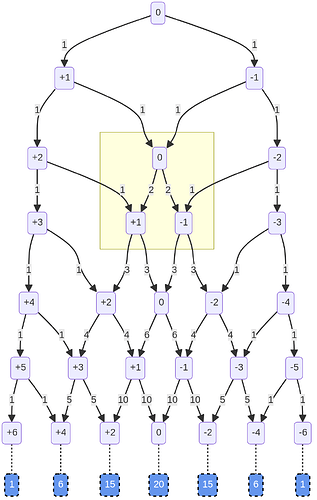
But there are two ways to get to 0: the path from the left (i.e. HT) and the path from the right (i.e. TH). If we add up the numbers on the paths pointing to a particular box, we get the number of ways to get to that heaviness in that number of flips.

And if you look at the paths coming out 0, each is labeled 2, the heaviness of the box they start from:

For example, the path on the left is the case where 1) we’ve flipped the coin three times, and 2) the first two flips left us with no imbalance, and 3) now we’ve flipped heads. That can happen if we flipped HTH or THH.

However, there are three ways to be at +1 heaviness after the third flip: HTH, THH, or HHT. Adding the paths flowing into that box gives us three, because there two ways to get to 0 on the second flip, and one way to get to +2.

Assuming you are with me so far, jump down to the 6th flip:

Here we can see that the possible paths to a given heaviness really adds up. There are 10 paths from -1 to 0 heaviness on the 6th flip, and 10 paths from +1 to 0, so if we’re balanced after the 6th flip, there will be 20 ways we could have gotten there.

For easy of reference, the total paths to each heaviness after the 6th flip are provided in the blue boxes at the bottom:

Here we see the net effect, and how this chart shows that the outcome can be both random and follow a predictable distribution. We already knew that there are 64 possible sequences of 6 flips (2^6) – of thos, 50 possible paths leave us with +2, 0, and -2, heaviness.

As with previous graphs, this was an assache to produce, but I fully expect the trend to continue as we add flips.

Without talking about probability at all, there are just more ways to have a balanced series of flips than an imbalanced series. Like if you just lined up coins on the floor in groups of six, and made every possible series of heads and tails, most of the lines would be close to an even mix of heads and tails.

I’ll write up a script to see how concentrated it gets, but hopefully the chart clarifies the point I’m making: the likely distribution depends on all the ways that distribution can be arrived at – what’s possible influences what’s probable.

[PZR]

@Carleas

This doesn’t follow. If each flip was 50-50, some would stay tails-heavy forever, some would stay heads-heavy forever, and some would go back.

Right, so now, you have made a falsifiable claim.

Go forth now and produce a 10 mill flip where it goes heavy and stays heavy. A single one, I only want one. You can do a million 10 mill flips if you want. Find me one example.

[PZR]

@Carleas

You’re going to hate this, but I made another chart:

You are right, I didn’t bother with any of them. Even though I can’t help admire the work that goes into them.

I’m not trying to be rude, but if you can’t put it into simple rhetorical language, you don’t understand it enough yourself to explain it to me from a graph.

[PZR]

Here, I cut out some of the work for you.

Edit fiddle - JSFiddle - Code Playground

It’s my same program but it counts heads heavy too.

As long as heads heavy and tails heavy each have at least 1, it came back from the heavy state.

[PZR]

Funny how life works.

You will find that, in instances where one heavy state is much smaller than the other, it will proportionally overrepresent the overall underrepresented instance by a far greater margin, every time that I could detect but eventually an exception would probably come along, than it will undercut the overrepresented overall instance.

Iow, a smaller tails heavy sample than heads heavy sample will give a proportion of tails heavy heads that outruns the proportion of overall heads by a far wider margin than heads heavy heads will underperform overall heads.

[PZR]

Mast be magic, man.

[Flannel_Jesus]

Really well illustrated. And if you follow the pathways down, it’s so obvious that many pathways swap sides. It’s also obvious that only one of the many pathways is all tails, and only one is all heads.

[PZR]

Is a coin more likely to flip tails of it has already flipped heads a bunch?

You’re goddamn right.

[PZR]

By the way, this means that if you notice that a heavy series is outperforming the overall series by more than a certain amount, you can predict that it will likely be short.

Duh, conforming to an overall 50 50 balance.

What does this mean for a per flip calculation?

Hm.

It means that a flip preceded by a series that is fairly balanced, then sharply imbalanced, is more likely to be the result opposite the imbalance than a similar flip with a similar imbalance, but which had a more balanced overall preceding series, rather than fairly balanced and then suddenly sharply imbalanced.

Whiplash, if you will.

[PZR]

I’m giving you bastards too much.

[Carleas]

@PZR

Go forth now and produce a 10 mill flip where it goes heavy and stays heavy.

@PZR

You are right, I didn’t bother with any of them.

Yeah, it shows.

Here’s a program that does what you’re asking for. It iterates sequences of 10m flips, adding +1 or -1 to a balance variable. If it gets through all 10m flips without returning to 0, it scores a success, otherwise it’s a failure.

All Heavy - JSFiddle - Code Playground

I get about 2 successes every 10k iterations (.02%). That seems in line with the explanation in my last post.

@PZR

Is a coin more likely to flip tails of it has already flipped heads a bunch?

This is the program that tests that question directly:

@Carleas

Here is a program that samples one flip from a bunch of permutations, in order to avoid the th-sequence problem. For each permutation, it flips coins and counts heads and tails. If tails ever exceeds heads by a random amount between 0 and 100 (to make sure we aren’t only looking at tails=heads+1), it flips one more coin and increments thHeads or thTails.

[PZR]

You call that directly?

Directly is;

flip a bunch of times

Find the times that fit

@PZR

of it has already flipped heads a bunch?

Count them.

Compare them to when it has not

@PZR

of it has already flipped heads a bunch?

See if there is a difference in likelihood.

That is direct.