Lately, my head has been up in space–well, not literally, but I’ve been thinking of space–spacetime, that is.
I’m thinking of all the ways in which it can bend, warp, curve, distort, and even fission (sometimes there can even be “rips” in the spacetime continuum–or wormholes! Or blackholes! [size=85]Or asshole… well no.[/size]). In essence, space isn’t just “flat”–it’s more dynamic than that. (see Einstein and company for proof.)
So this got me thinking: what kinds of patterns are possible in the fabric of spacetime? I mean, if it’s not just flat, what other patterns could it take?
To be sure, the only alternative patterns to a flat spacetime that Einstein offered for the universe were: a 4D sphere or a saddle-shaped plane (or surface–I’m not sure, but I think a “plane” is technically defined as flat).
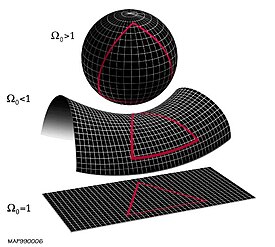
But I think we can be more creative than that.
I forget who proposed it, but I remember once reading Brian Green’s The Elegant Universe and he referenced a geometrical model of the universe made famous by a thinker who’s name escapes me now. It features an actual finite limit to a 3 dimensional space (such that the “edge of space,” as it were, is a finite distance away), but that as one approaches this outer limit, space becomes more “dense” or “thick”–that is, if you were to map a geodesic of space from you (at a specific point in time as you travelled towards the edge of space) to the actual edge of space, the distance between the tick-marks on that geodesic (as if it were a ruler) would have to be drawn more closely together the closer you got to the edge of space. The end result would be that, though you always approach ever closer to the edge of space, your speed slows down… and you never really reach the end of space–it’s an “infinite” distance away for all practical purposes.
Now, that’s just one pattern.
There are others: wormholes present a pattern whereby the universe might conceivably feature parallel planes linked together by a wormhole (looking like an apple core). Of course, these “planes” would really be 3 dimensional, and the wormholes would project out into a fourth dimension of which we have no way of experiencing (hey, this is all Einstein, not me). Then there are blackholes, points in space towards which spacetime converges–but kind of in the opposite way from the model I relayed above (the one whereby space becomes more “dense” the further out you go). In this pattern, you get space getting “thinner” the closer you get to the center of the blackhole, and thus things travelling towards it accelerate.


But the thoughts that I’ve been having lately have been more along the lines of repeating patterns.
To be fair, there are models of spacetime geometry that feature complex detail–as opposed to smooth and simple patterns only interesting when seen at a cosmological level–and I’m reminded of what they call “quantum foam”. Quantum foam, if I understand it correctly, is a model of spacetime in which, way down at the subatomic level (at the “quantum” level, as they say), spacetime is really bumpy–it isn’t smooth as we experience it here at the macro-level–instead it’s more like “foam”–twisting and winding geodesics, all intersecting, merging, bending, blending, splitting, splicing, separating, connecting, rising, falling, growing, shrinking, etc., etc., etc.–basically like a fur ball a cat coughed up (except the strands of fur are infinitely long).
Interesting pattern.
But still, there is no repetition. What if spacetime were more like a checker board–you can even imagine it as a 3D checker board–with cubes instead of squares–like Q-bert!

Each cube-like section of spacetime would be characterized by either of two features, and those two features can be anything you like. For example, say all the odd squares had “thin” space, and all the even squares had “thick” space. That’s it–there you go–the cosmic checkerboard!
But, you say, wouldn’t we notice differences as we pass in and out of these two kinds of spacetime cubes? Wouldn’t things behave differently somehow as they passed in and out of these cubes? Well, that depends–how subtle is the difference? Remember, I only said the odd cubes were “thin” and the even cubes “thick”–I never said drastically thin or thick. The degree to which they differ may be so unnoticeable that it’s several magnitudes smaller than the Plank scale. Or how about this: the difference may be great, it may be staggering, but the cubes are absolutely, extraordinarily, utterly tiny–smaller than the Plank scale–that not even the electrons and quarks that make up our bodies undergo a disturbance as they pass through them.
How about a pattern like a Persian rug? How about a complex computer circuit? How about a fractal?
