In my previous post about Quantum Mechanics, I mentioned Bell’s Theorem in passing. However, this is one of the most fundamental aspects of Quantum Theory and understanding it was a fully mind-blowing moment for me, at least as mind blowing as the double-slit experiment. So I thought I’d come in here and give some more background and an explanation for what I said in the other thread, that the experiments validate Bell’s Theorem that “hidden local variables” can’t account for the statistics we see with entangled particles.
A bit of historical background: when Quantum Mechanics was first coming to the attention of theoretical physics, it had a lot of pushback, and for precisely that reason: that it seemed to imply some sort of non-local causality. Einstein himself objected to it, and played a central role in formulating the EPR Paradox paper in1935:
It wasn’t until 1964 (unfortunately years after Einstein’s death) that someone devised an experiment that could prove which side of that debate was right - and it would bbe years after that until those experiments would be actually performed. John Stewart Bell noticed that, using the correlations predicted by Quantum Mechanics for the spin of photons, you could devise a set of experiments which would be impossible to reproduce using classical assumptions. This was Bell’s Theorem.
First, about measuring spin with singlet-state entangled photons, and setting up our toy experiment
In very basic terms, when two photons (or electrons) are entangled in a singlet-spin-state way, then when you measure one photon’s spin as up, the other one is always down. However, note that you can measure spin at any angle, but you can only get a positive or negative result for that angle.
To help visualise this, what I’m going to do is describe to you a completely non-quantum classical experimental setup that should fully mirror the Quantum tests at a conceptual level.
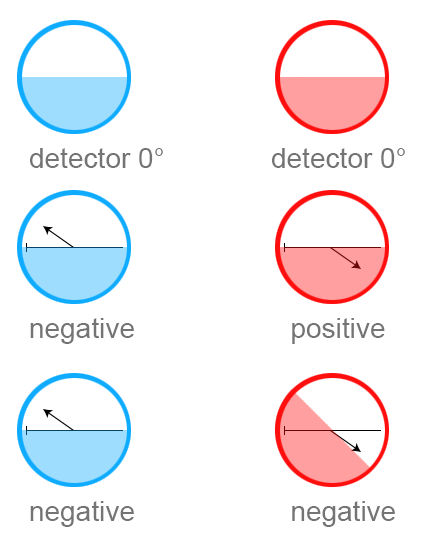
Imagine you have a bag of millions balls. Each ball has two halves - red and blue - and you can pull the ball apart and see, on each inner side, an angle represented. And, just like with the electrons that have always opposite spin, the angle in these balls is always opposite as well - 180° from each other. An illustration:
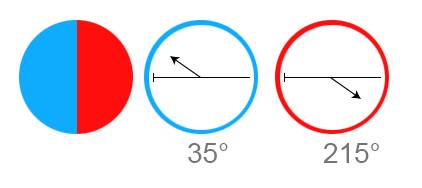
And just like with the electrons, with these balls we’ll invent a measuring apparatus - a detector that can be rotated to any angle. Each detector can only give you a “positive” or “negative” result - “positive” if it’s in the coloured area of the detector, negative otherwise. When the two detectors are set at the same angle, the have opposite results 100% of the time. When one is set to 180° of the other one, they have the same results 100% of the time. However, other angles in between only have a certain percent chance to match, based on the angle. In this example, if you rotated the Red detector to 45° but kept the blue one at 0, you’d see a double-negative result:
(you may have to scroll to see the full image) In order to fully match the quantum experiment, when they’re running the experiment with the balls, the experimenters aren’t allowed to look at the angle, they can only use the measurement device to get a negative or positive. And we can only measure each one once.
Now, if you’re an experimenter with these balls, you wouldn’t be able to take that double-negative result and know which exact angle either ball is at, BUT we know that, because the balls are entangled, the measurement of the red ball tells us something about the blue ball, and vice versa – we know that IF we had instead measured the blue ball at 45deg, we would get a positive, since red gave negative. And we know that IF we had instead measured the red one at 0deg, we would have a positive there too, since the blue gave us a negative.
So now that we know how the balls work and how the detectors work, we can start…
Running the actual experiment
We’re going to run an experiment on our physical balls, but ALSO simultaneously we’re going to have some physicists run the same experiment on their photons, and we’ll compare results after.
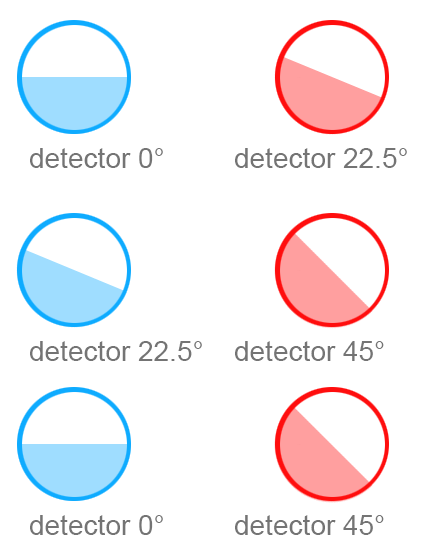
The experiment works like this: First, I set up my blue detector at 0° and I set up my red detector at 22.5°, and I send as many balls as I can stand to wait for through to be measured, and I count how many of them come out positive on both red and blue. Then, I rotate my detectors: blue detector at 22.5°, red detector at 45°, and again I send as many as I can through and count how many come out positive on both. Then, I rotate my detectors one more time, this time blue is at 0° and red is at 45°, and once again I send as many as I can through and count how many come out as ‘positive’ on both.
And of course I ask my physicist friends to do the same with their photons - they’ve got a blue and a red spin detector to
What we find with our blue and red balls is:
Setup 1, 0° and 22.5°, out of 10,000 balls sent through, 625 have come back with both detectors positive (6.25%)
Setup 2, 22.5° and 45°, also has 625 out of 10,000 balls come back with both detectors positive (6.25%)
Setup 3, 0° and 45°, has 1250 out of 10,000 balls come back with both detectors positive (12.5%)
Nothing out of the ordinary there!
However, oddly, our physicist friends got a … different result
Setup 1, 0° and 22.5°, out of 10,000 photon-pairs sent through, 732 have come back with both detectors positive (7.32%)
Setup 2, 22.5° and 45°, also has 732 out of 10,000 photon-pairs come back with both detectors positive (7.32%)
Setup 3, 0° and 45°, has 2500 out of 10,000 photon-pairscome back with both detectors positive (25%)
The paradox is in there, but we’ll have to do some work to get it out
We need to look a bit more closely at the results the physicists got, because there’s a paradox in those results that isn’t entirely obvious at first glance. This paradox is at the heart of Quantum Mechanics.
Consider setup 1: of all the photons that went to the red detector, 732 were positive at 22.5°, but their sister-photon was positive at 0°, which means the red ones would have been negative if they were measured at 0°
setup 2 as well: 732 photons sent to the red detector that were positive at 45° but would have been negative if they were measured at 22.5°
setup 3: 2500 photons to red, all positive at 45°, all would have been negative if measured at 0°
These 2500 photons have a problem: we didn’t measure them at 22.5°, but we know that IF WE HAD, they would have been either positive or negative if we did.
We know they’re positive at 45°, we know they’re negative at 0°.
Imagine if we split this 2500 into two groups: those that would have been positive at 22.5°, or those that would have been negative at 22.5°.
We can deduce that the half that would have been positive at 22.5° would have passed in setup 1.
We can deduce that the half that would have been negative at 22.5° would have passed in setup 2.
Which means EVERY photon that passed in setup 3 should theoretically either pass in setup 1 or setup 2.
Which means the sum of the passes in setup 1 and setup 2 should be AT LEAST equal to the passes in setup 3.
But they’re not. They’re not even close. 732 + 732 is 1464, nowhere near the 2500.
But this is the result that QM predicts, and this is the results that experiments prove.
So those are the numbers, and they don’t add up, but what does that mean?
The reason why this is important is, no matter what way you try to arrange my classical balls, there’s no way to get an experimental result like this. There’s no way for the balls to have a fixed angle of spin as they separate from each other, that produces these numbers. No matter how you fix the angle of spin in the classical balls, the number of balls that pass setup 1 and setup 2 will always add up to setup 3 perfectly.
And reality seems to match what Quantum Mechanics predicts in this case, not our classical ideas of fixed properties that get measured later. That’s why “Bell’s theorem proves that quantum physics is incompatible with local hidden-variable theories.” The spin of these entangled photon cannot be fixed at the time of entanglement, and also produce the measured results we get. The numbers don’t add up for that to be the case.