My notes on this video as I learn. Please scan for questions & correct any false inferences.
categories without elements (instead: constructions of arrows between objects, showing how they relate)
three rules for categories:
composition (for implementation)
identity/unit (object with arrow pointing back to itself)
associativity (can be composed in any order) (concatenation of strings)
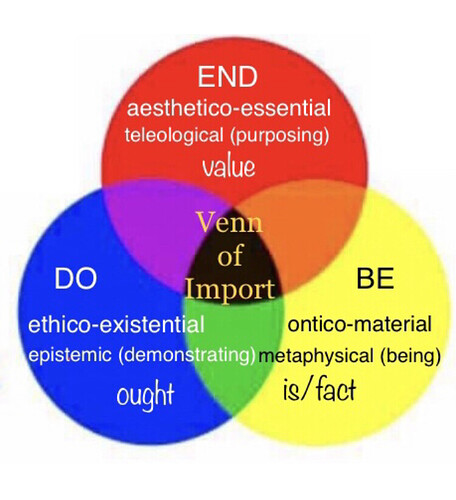
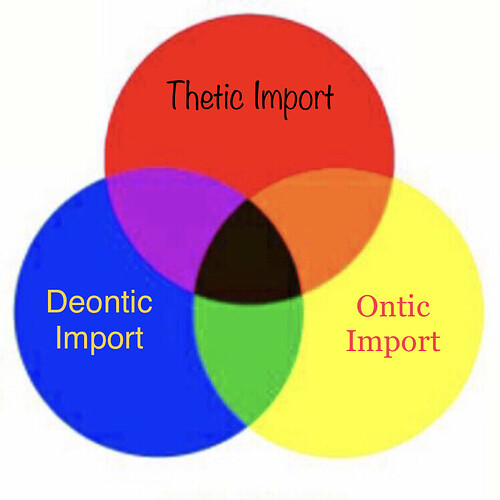
Kleisli category has same objects but different arrows from the ones in Category C (a monad). is this also a correct representation of what Leibniz meant by monad? Or is it only the red sphere of a monad (if the Venn of import is what was meant by a monad)?
object a in category C becomes type (or object) “a, string”, or m a (map a) or f a (functor a), and there is an embellished arrow between a adjacent to “m b” (from object b) in Category C that becomes a direct arrow in the Kleisli category (a down to b). This implements a function in category C to the Kleisli category.
instead of sets having elements or being empty, categories have defined objects according to universal composition (how everything relates to everything else) — it focuses not on the physical parts of an object (which becomes important when you’re talking about patterns/properties rather than substance/actualization) but on its properties in relation to other objects
there is only one case in which there is no arrow, from a non-empty set to void (empty set) because there is no image to point to in the void. Except in the case of the void, every set functionally relates/connects to every other set.
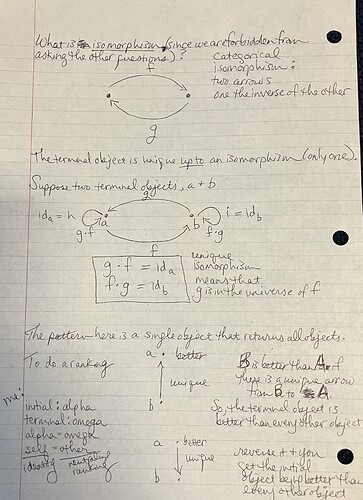
singleton set usually has one element, but instead of talking about elements, we say that it has an arrow pointing from every other set to itself, including from itself to itself (unit/identity) — this is a terminal ¿object/set? - all arrows FROM other ¿objects/sets) — but there is only one true path or arrow to the terminal object. bool is true/false … at least two arrows …. but there are more arrows when there are predicates.
There is only one unique isomorphism between two terminal objects.
If having an arrow to an object means this object is less than or equal to the object to which it points, the object to which they all point is the highest ranked object. (So there is no terminal object in the set of natural numbers.)
initial ¿objects/sets? (arrows TO all other ¿objects/sets?) - empty set - void - the arrow is “absurd” & it also points to itself as unit/ID. rather reminds me of creation ex nihilo - but that implies propertyless substance. Maybe instead it should remind me of capacity or intention? formal/final is (beginning/alpha) initial/terminal (end/omega)
I don’t know yet what it means when he says “ignore the argument“ — I didn’t start at the beginning.
mentions identity of indiscernibles (Liebniz) w/o saying it
pattern=object in a category
ranking=If you say “a is better than b if there is a unique arrow from b (etc) to a” you will return a terminal object. If you say a is better than b if there is a unique arrow from a to b” you will get an initial object.
self=other or terminal=initial means every object in the category has the same ranking